A couple months ago, when I was writing some code to implement a text editor, I was thinking about how I should design the data structure to map a character offset to a line number and column, and vice versa. I ended up designing what might be a novel data structure, along with several other data structures that other people have almost certainly also come up with. I benchmarked the three, and found that my data structure, while having some substantial benefits, also had a substantial drawback. I'm posting this partly because it's interesting, and partly in the hope that some smart person can comment on it.
The first data structure that popped into my mind was the simplest one -- an array, indexed by line number, storing the starting indices of the lines. The length of a line could be calculated by taking the difference between neighboring starting indices. With this array implementation, adding a new line to the end of the array and converting from line number to starting index are O(1) operations, but everything else is O(N). I quickly realized that it might be improved by storing the length of each line rather than the starting index of each line. Doing so means that changing the length of a line -- obviously a very common operation in a text editor -- becomes O(1), while converting a line number to its starting index becomes O(N). The array implementation has the benefit of being very simple, and I suspect many text editors use it.
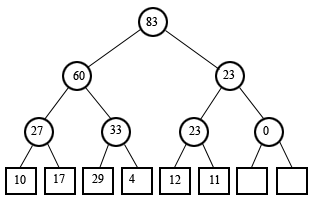
(the same thing in tree form)
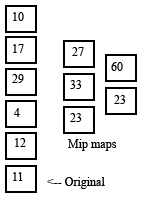
(mip maps)
The upside to this data structure is that many operations that are O(N) in the array implementation are O(log N) in the tree implementation. Retrieving the length of a line remains O(1). However, some operations that are O(1) with the array, such as updating a line length, become O(log N) with the tree. Also, the space requirements are doubled compared to the array. Inserting, deleting, and adding lines are the slowest operations with this data structure. Although both the tree and the array have O(N) insertion and deletion time, the constant factors in the tree implementation make it take about six times longer. But I was confident that it was better than the array for large numbers of lines, because querying should be much more common than inserting and deleting lines.
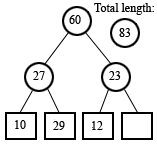
(a compressed version
of the above)
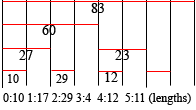
(the spans of lines summed
for each tree node)
Given this revelation, I had an idea for how to query the data structure. Consider line number 3 (with zero-based counting). We know that the line has a length of 4. Here's how to calculate that from the tree. The line index 3, in binary, is 011. We start by positioning a node pointer to the leaf node nearest to the line we're looking up. The length of line 3 is not stored directly, but line 2 is, so we'll start there. We can simply mask off the LSB to get this index. In the tree above, you can see that line 2's length is 29. That's where the node pointer begins. We'll have a value that accumulates the length of the line, initialized to zero. If the LSB of the index is 1, we subtract the value stored at the node from the accumulator, shift the index to the right, move the node pointer up to the parent node, and repeat. If the LSB is 0, we add the value to the accumulator and the calculation is complete. Remember we have index 3, with binary representation 011. Since the LSB is 1, we subtract the current node value, 29, from the accumulator. The index is right-shifted, becoming 01, and the node pointer is moved to the parent, which stores the value 27. The LSB is still 1, so we subtract again. The accumulator becomes -56, the index becomes 0, and the node pointer moves to the node storing 60. The LSB is now equal to 0, and so we add 60 to the accumulator. -56 + 60 = 4, which is the length of the line. The offset of a line can be calculated very similarly, and simultaneously in fact. (You may notice a special case when retrieving the length of a line with an index that has all relevant bits set to 1, for instance the line at index 7 (binary 111) in a tree that can hold 8 lines. By the time the LSB of the index becomes zero, the node pointer has moved above the root of the tree. The elegant solution is to add a node above the root of the tree that stores the total length of the document (ie, a new root with only one child, which is the binary tree in the picture).
With that much worked out, it was also easy to figure out how to go the opposite way, converting a character index into a line number, by starting at the root of the tree and working downwards.
But I still didn't know how to update the data structure efficiently. Updating the length of a line seemed easy enough -- just propogate the length difference up the tree, adding it to the node value wherever a zero bit is found in the line index. But inserting and deleting lines efficiently has me stumped. Since the bottom row in the tree stores only the lengths of even-numbered lines, inserting or deleting a line causes all of the line numbers after it to be shifted by one. Even-numbered lines become odd-numbered, and vice versa. Since the lengths of odd-numbered lines are not stored directly in the tree, all of the new values for the leaf nodes after the insertion point would have to be recalculated. In my implementation, they are recalculated using the algorithm given above to retrieve a line length. This makes line insertion and deletion take O(N log N) time. It may be possible to recalculate them incrementally, but thinking about it made my brain hurt. Can you think of a faster way to insert or delete a line?
Complete source code and benchmarks for the data structures discussed are included in this source file. On the upside, the fancy tree structure is a bit faster than the simple tree structure at querying line information, and surprisingly, is orders of magnitude faster at adding lines to the end. And it only needs half as much space. On the downside, the benchmarks show the fancy tree structure taking 6 ms per line insertion/deletion compared to 0.31 ms for the simple tree structure, a factor of 19.4 difference, for trees holding 100,000 lines. Both the factor of the difference and the absolute times involved are substantially reduced for trees holding more typical (ie, smaller) numbers of lines, but even so, I was ultimately dissuaded from using my data structure because of its asymptotic complexity with regard to insertion and deletion.
Comments